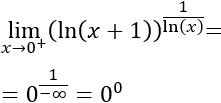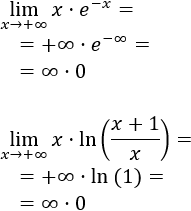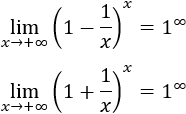MATEMÁTICAS: LÍMITES

MATEMÁTICAS: LÍMITES
Las indeterminaciones en matemáticas son expresiones que surgen en el cálculo de límites y no tienen un valor definido o claro sin un análisis adicional. Estas expresiones pueden adoptar varias formas y suelen aparecer en situaciones donde el comportamiento de una función o una fracción es ambiguo cuando se acercan a ciertos puntos. A continuación, se explica en detalle qué son y cuáles son las formas más comunes de indeterminaciones:
Esta forma aparece cuando tanto el numerador como el denominador de una fracción tienden a cero. Por ejemplo, el límite de f(x)/g(x) cuando f(x)→0 y g(x)→0.
Ocurre cuando tanto el numerador como el denominador tienden a infinito. Por ejemplo, el límite de f(x)/g(x) cuando f(x)→∞ y g(x)→∞.
Esta forma se presenta cuando se resta un infinito de otro infinito, por ejemplo, lim x→∞(f(x) - g(x)) cuando ambos f(x)→∞ y g(x)→∞.
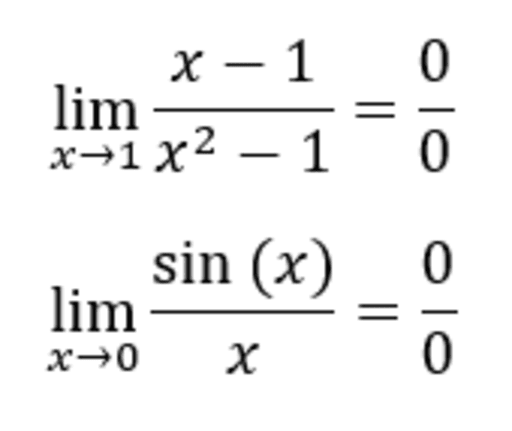
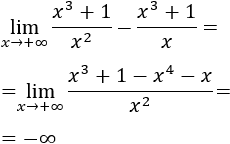
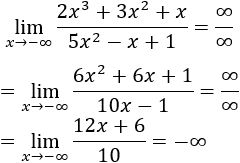
Aparece cuando un término tiende a cero y el otro a infinito, como lim x→a f(x)⋅g(x) cuando f(x)→0 y g(x)→∞.
Se presenta en límites exponenciales donde la base tiende a uno y el exponente a infinito, por ejemplo, lim x→a [f(x)]^g(x) donde f(x)→1 y g(x)→∞.
Ocurre en expresiones donde una base que tiende a cero se eleva a una potencia que también tiende a cero, por ejemplo, lim x→a [f(x)]^g(x) donde f(x)→0 y g(x)→0.